dev-miri
[Data Structure][자료구조][C++]Priority Queue 그리고 Heap 본문
자료구조 수업시간에 배운 중요한 개념인 Priority Queue와 Heap을 정리해보려고 합니다.
1. Priority Queue
1)Queue
Priority Queue에 대해 설명하기 전, Queue의 개념에 대해 간단하게 알아보겠습니다
[자료구조][C++][TIL]Stack&Queue
컴퓨터공학과 전공과목 자료구조 3, 4주차에 Stack과 Queue를 공부하였습니다. Stack과 Queue에 대한 개념과 구현방법을 공부하고, 관련된 백준 문제를 풀어보았습니다. Stack 1. 스택이란? -접시를 쌓듯
devmiri.tistory.com
앞선 글에서 Stack과 Queue의 개념을 설명하고 구현해보았으니 참고해주세요!
이름으로만 보면 Priority Queue가 Queue에 속하는 하위항목으로 생각되지만,
Priority Queue가 Queue보다 더 general한, 즉 Queue가 Priority Queue의 일종이라고 합니다!
Queue를 한마디로 정리하면 FIFO(First In First Out), 즉 선입선출 구조로
먼저 삽입된 객체가 먼저 삭제될 수 있는 자료구조 입니다.
2) Priority Queue(우선순위 큐)
우선순위 큐는 엔트리의 collection을 저장하는 자료구조입니다.
기존의 Queue의 FIFO를 사용하지 않고, 들어간 순서에 상관없이, 우선순위에 따라 결과가 달라집니다.
엔트리는 value v와 키 k로 이뤄진 쌍 (v, k)입니다.
그럼 '우선순위'는 무엇일까요? 엔트리의 키(key)k는 우선순위를 나타내며, 그 키는 사용자가 결정합니다.

출처 : Data structures and algorithms in C++
-insert(e) : insert 함수는 element e를 삽입하는 함수로, queue의 enqueue연산입니다. 뒤에서 언급할 삽입정렬, 선택정렬의 경우에 따라 insert연산은 key의 영향을 받을 수도 있고, 받지 않을 수도 있습니다.
-min() : 우선순위 큐에서의 가장 작은 key value를 가진 element e를 반환하는 함수입니다.
max가 아닌 min함수인 이유는 우선순위 큐에서는 key가 작을수록 우선순위가 높기 때문입니다.
-removeMin() : min()의 element를 우선순위 큐에서 삭제하는 함수입니다
-이 외에도 크기를 리턴하는 size()함수와 비어있는지 확인하는 empty()함수가 있습니다.
3)Total Order Relations
우선순위 큐에서 key의 크기가 작을수록 우선순위가 높다는 특징을 가지고 있습니다
즉, key는 순서가 정의될 수 있어야 합니다.
key의 순서를 정의하는 비교규칙이 항상 적용되기 위해서는 전체 순서 관계(total order relation)를 만족해야 합니다.
모든 쌍의 두 키에 대해서 아래와 같은 특성을 만족해야 합니다
1. 반사성(Reflexive property) : k<=k
2. 비대칭성(Antisymmetric property) : 만약 k1 <= k2이고 k2<=k1일 경우 k1=k2
3. 이행성(Transitive property) : 만약 k1 <= k2이고 k2<=k3일 경우, k1<=k3
보기에는 당연해보이는 특성들이죠? 모든 쌍들의 key가 이러한 성질들을 전부 만족해야한다는 것을 기억하면 됩니다!

A는 C에 속하고, C는 D에 속하므로 3번 규칙 이행성에 의하면 A는 D에 속한다는 결론을 낼 수 있습니다.
하지만 B, C는 비교할 수 있는 대상이 아닙니다. 즉, 1, 2, 3번 규칙 모두 만족시킬 수 없습니다.
즉 Total order realtionship이 아니라는 것입니다.
(Parital Order Realationship이라는 개념도 존재합니다. 부분적으로 이 규칙들을 만족시키면 Partial order realtionship이라고 볼 수 있습니다. 즉 집합 S는 Partial Order Relationship입니다.)
4)우선순위 큐 구현하기
우선순위 큐를 구현하는 방법에는 크게 두가지가 있습니다.
첫번째는 시퀀스(Sequence)를 사용하여 구현하는 방법,
두번째는 힙(Heap)을 사용하여 구현하는 방법입니다.
먼저 시퀀스를 사용하여 구현하는 방법을 알아보겠습니다.
4-1)시퀀스로 우선순위 큐 구현하기
시퀀스로 우선순위 큐를 구현하는 방법에는 두 가지가 있습니다.
첫 번째는 정렬되지 않은 시퀀스(Unsorted Sequence)를 이용하는 방법,
두 번째는 정렬된 시퀀스(Sorted Sequence)를 이용하는 방법입니다.
4-1-1)Unsorted Sequence로 우선순위 큐 구현하기
-Insert(e) : 원소 e를 우선순위 큐에 삽입하는 함수 O(1)
- 원소를 벡터의 마지막에 추가
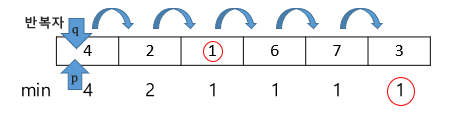
-removeMin : 가장 작은 키를 갖는 원소 e를 제거하는 함수
- 우선순위 큐에 저장된 데이터들과 우선순위를 비교
- 반복자 q를 이동하면서, 가장 작은 키를 갖고 원소를 가리키는 반복자 p를 갱신
4-1-2)Sorted Sequence로 우선순위 큐 구현하기
-Insert(e) : 원소 e를 우선순위 큐에 삽입하는 함수
- 큐에 저장된 데이터들과 우선순위를 비교하고, 삽입될 위치를 찾는다
- 삽입될 위치를 확보하기 위해 벡터의 원소를 옮긴다

-removeMin : 가장 작은 키를 갖는 원소 e를 제거하는 함수
- 삽입할 때 이미 정렬된 상태이므로, 맨 뒤의 원소를 큐에서 제거
4-2)힙으로 우선순위 큐 구현하기
4-2-1)힙(Heap) ->이 글은 우선순위 큐에 대한 글이므로 heap에 대한 개념은 다음 글에서 다룰 예정
- 힙이란? 아래의 2가지 property를 만족하는 binary tree
- complete binary tree : 마지막 level을 제외한 나머지 level에 node들이 가득 차있고, 마지막 level에서 node는 가장 왼쪽부터 채워지는 형태
- heap-order : 트리의 내부 노드는 우선순위를 만족해야 한다
- Min-Priority Queue=>key(parent(v))<=key(v)
- Max-Priority Queue=>key(parent(v))>=key(v)
- 힙 기반 priority Queue
- (ex)Insert 2 to Min-Heap
- 유념해야할 점은 Heap을 유지해야 한다!
- Complete Binary Tree
- Heap-Order
- 유념해야할 점은 Heap을 유지해야 한다!
- (ex)Insert 2 to Min-Heap

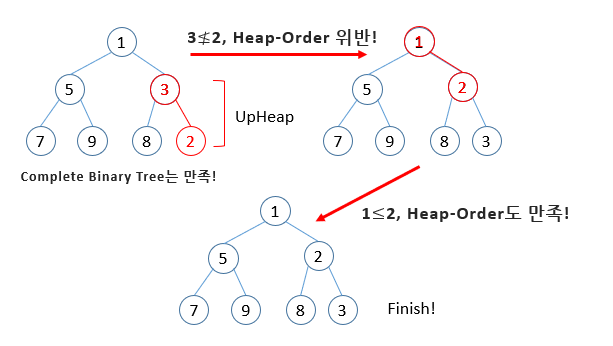
- (2)를 삽입한다
- UpHeap 과정을 거친다(heapify->heap이 아닌 구조를 heap으로 바꾸는 과정)
- (ex)removeMin to Min-Heap - root에 있는 1을 삭제하고 싶다면?
- Heap을 유지해야 한다!


- 삭제 하고자하는 루트의 1을 가장 마지막 원소인 3과 위치를 바꿔준다(swap)-루트는 임의로 삭제가 불가능하다
- 1을 삭제한다
- 3의 downheap 과정을 거친다(complete binary tree는 만족하였으나, heap-order은 만족하지 않음)
5) 우선순위 큐를 이용한 정렬
- 전체 순서 관계에 따라 비교될 수 있는 n개의 원소들의 집합 L을 가정하고, 집합 L을 우선순위 큐 P를 이용하여 정렬한다.

- 선택 정렬 구현
- 비어있는 우선순위 큐 P에 집합 L의 원소들을 n번의 연속된 insert 연산에 의하여 삽입한다
- removeMin 연산을 n번 연속 이용하여 우선순위 큐 P에서 원소를 집합 L에 다시 넣는다
- 이때의 removeMin 연산에서 원소를 작은 순서대로 선택해 집합에 넣음으로써 정렬한다

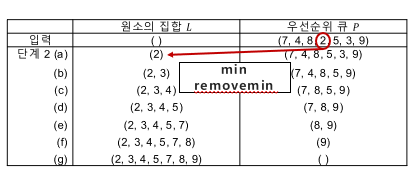
- 삽입 정렬 구현
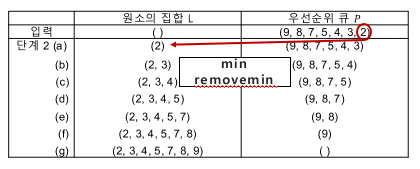
- 비어있는 우선순위 큐 P에 집합 L의 원소들을 n번위 연속된 insert 연산에 의하여 삽입한다
- 이때의 inserst 연산에서 우선순위 큐에 원소를 순서대로 삽입함으로써 정렬한다
- removeMin 연산을 n번 연속 이용하여 우선 순위 큐 P에서 원소를 집합 L에 다시 넣는다
- 이미 우선순위 큐에서 정렬되었으므로 그대로 집합 L로 옮긴다
- 비어있는 우선순위 큐 P에 집합 L의 원소들을 n번위 연속된 insert 연산에 의하여 삽입한다

- Insert/removeMin의 시간복잡도
| Unsorted Sequence | Sorted Sequence | Heap | |
| Insert | O(1) | O(n) | O(logn) |
| removeMin | O(n) | O(1) | O(logn) |
'CSE > Data Structure' 카테고리의 다른 글
| [자료구조][C++][TIL]Stack&Queue (0) | 2022.03.27 |
|---|

